Metatron’s cube is not a two-dimensional image that hangs on the wall. It is not flat and motionless. It is three-dimensional in our world and full of movement and energy. Understanding it as a “key to creation” holds great promise for our third-dimensional world. We need a more accurate model, a three-dimensional figure for our investigations into Metatron’s cube.
We have a two-dimensional image of Metatron's cube that is a starting point for understanding the true nature of Metatron’s cube. That image is shown below.
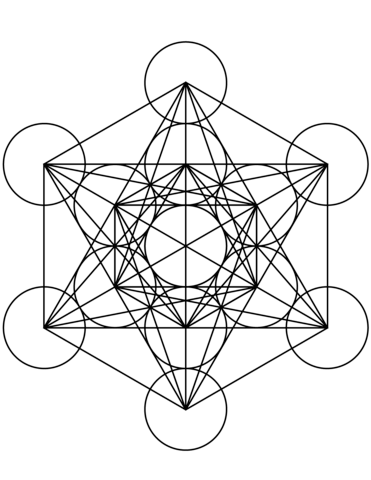
The five Platonic solids are all contained within this two-dimensional image. When you attempt to visualize the Platonic solids, they are, of course, also shown in two-dimension.
Here is what I have been told. “Metatron’s cube is a key, a key to creation. A key to the molecular changes, the energy. A force so great and renewable. Your entire world has the potential to change, to be completely reinvented.” How do we unravel the secrets that Metatron’s cube contains?
In order to more effectively study Metatron’s cube, we need to have a more accurate visualization of it. That is why I have created the following videos that show how to expand Metatron’s cube into a three -dimensional model.
Let’s begin with extracting the tetrahedron from the two-dimensional image of Metatron’s cube. You might notice that there are tetrahedrons everywhere. Some are smaller than the others. The larger ones tend to be easier to see. Some are inverted. There is a smaller tetrahedron that points to the center of each circle. Click on the video below which focuses on the larger tetrahedron to see the animation of it turning into a three- dimensional shape.
The next blog will show the extraction of the hexahedron and the octahedron from the two-dimensional image of Metatron’s cube. The three-dimensional model that we are working to build is shown below.

You can see the orange-colored three-dimensional image of the larger tetrahedron. It looks inverted in this image. You might also notice some smaller ones closer to the middle of the cube.
Comments